
Home
Common Compounds
Exam Guide
FAQ
Features
Glossary
Construction Kits
Companion Notes
Just Ask Antoine!
Simulations
Slide Index
Toolbox
Tutorial Index
Introduction
Measurement
Matter
Atoms & ions
Compounds
Chemical change
The mole
Gases
Energy & change
The quantum theory
Electrons in atoms
The periodic table
Chemical bonds
Solids
Liquids
Solutions
Acids & bases
Redox reactions
| Reaction rates |
Everyday chemistry
Inorganic chemistry
Environmental chemistry
Laboratory
History of chemistry
Miscellaneous
Home  FAQ FAQ  Reaction rates Reaction rates | Print | Comment |
| Previous Question |
Does a 10°C temperature rise double reaction rates?
- I believe there is an equation that demonstrates the relationship between the change in temperature and the rate of reaction, in essence,"for every 10 degree centigrade change in temperature the rate of reaction will half or double." I cannot find the source or correctness of this concept...can you help?
Thank you. John J. Baccelli,D.D.S. 11/29/99 -
The assertion that "a 10° temperature rise doubles reaction rates" is just a rule of thumb, not a law of nature. Like most rules of thumb, "thumbtimes it works, and thumbtimes it doesn't." In fact, relying this rule to predict the effect of temperature on the rate of a chain reaction can be a catastrophic mistake.
Vocabulary activation energy 
Arrhenius equation
collision frequency
elementary reaction
equilibrium
exothermic
rate constant
reaction rate
universal gas constant
What is the source of the rule? The rule probably began with a back-of-the-envelope calculation based on the Arrhenius equation, first published in 1889. Arrhenius explained the variation of rate constants with temperature for several elementary reactions using the relationship
k = A exp(-Ea/RT)
where the rate constant k is the total frequency of collisions between reaction molecules A times the fraction of collisions exp(-Ea/RT) that have an energy that exceeds a threshold "activation energy" Ea at a temperature of T (in kelvins). R is the universal gas constant.To see what temperature rise is required to change the rate constant from k1 (at T1) to k2 (at T2), take the ratio of the Arrhenius equations for each of the two temperatures:
k2
k1= A exp(-Ea/RT2)
A exp(-Ea/RT1)= exp ( - Ea
R[ 1
T2- 1
T1]) - What activation energy must the reaction have to apply to make the rate double with a 10°C rise?
- Is the same activation required to make the rate quadruple for a 20°C temperature rise?
- Try a different initial temperature. Will the activation energy required be the same for any 10°C rise, no matter what the initial temperature is?
If the activation energy has a particular value, and if the temperature change occurs in the right range, and if the reaction is an elementary one that obeys the Arrhenius equation, then a 10°C rise might double the reaction rate. It's a very iffy generalization.
Can we at least say that reaction rate increases with temperature? For reactions that occur in a single step involving a molecular collision of some kind, the answer is yes. Only molecules with sufficient energy are able to react. Heat increases the average energy of the molecules and so it would be expected that reaction rate would always increase with increasing temperature.
But many reactions aren't that simple, and their rates may actually decrease with increasing temperature.
What are some examples of reactions that slow down when temperature rises? Nearly all biochemical reactions, for example, are catalyzed by rather delicate protein molecules called enzymes. Warming a biochemical reaction increases its rate as expected - up to a certain temperature. Heating beyond that point actually decreases the reaction rate and further heating can stop the reaction completely. Heat causes the enzyme to unravel or unfold, and the enzyme's shape is critical to its ability to accelerate the reaction.
Even some inorganic reactions can slow down when things heat up. Consider this reaction with intermediate B:
A 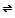 B
B(fast, exothermic) B 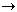 products
products(slow) 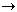 products will decrease as temperature rises.
products will decrease as temperature rises.
When can relying on the rule be dangerous? Consider the formation reaction for gaseous hydrogen chloride,
H2(g) + Cl2(g) The reaction requires heat (or light) for initiation: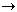 2 HCl
2 HCl
heat + Cl2(g) The extremely reactive chlorine atoms then trigger a chain reaction: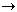 2 Cl(g)
2 Cl(g)
Cl(g) + H2(g) Notice that chlorine atoms are consumed in one step and produced in another. The reaction keeps going without further need for the initiation step.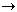 HCl(g) + H(g)
HCl(g) + H(g)
H(g) + Cl2(g)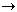 HCl(g) + Cl(g)
HCl(g) + Cl(g)
Heating the H2/Cl2 mixture will at first elevate the reaction rate only slightly. Once the propagation steps begin to occur at significant rates, further heating causes a sudden, tremendous acceleration in reaction rate. Instead of a doubling of rate that might otherwise have been expected, the rate may suddenly increase by orders of magnitude- resulting in a violent explosion!
Resources
Sorry, no matches were found containing the keyword:
General Chemistry Online! Does a 10°C temperature rise double reaction rates?
Copyright © 1997-2010 by Fred Senese
Comments & questions to fsenese@frostburg.edu
Last Revised 02/23/18.URL: http://antoine.frostburg.edu/chem/senese/101/kinetics/faq/temperature-and-reaction-rate.shtml