
Home
Common Compounds
Exam Guide
FAQ
Features
Glossary
Construction Kits
Companion Notes
Just Ask Antoine!
Simulations
Slide Index
Toolbox
Tutorial Index
Introduction
Measurement
Matter
Atoms & ions
Compounds
Chemical change
The mole
Gases
| Energy & change |
Electrons in atoms
The periodic table
Chemical bonds
Solids
Liquids
Solutions
Acids & bases
Redox reactions
Reaction rates
Organic chemistry
Everyday chemistry
Inorganic chemistry
Environmental chemistry
Laboratory
History of chemistry
Miscellaneous
Home  FAQ FAQ  Energy and chemical change Energy and chemical change | Print | Comment |
| Previous Question | Next Question |
How can the heat capacity of air be estimated?
- In order to work out a problem regarding the heating of a flow of air, I need two pieces of data that I can't seem to find.
1) What is the typical specific (or molar) heat capacity of air?
2) What is the typical density of air at, say, 10 degrees centigrade?
All books I have consulted give the above information for elements and single compounds only.
Matthew Hall -
You can find both of these items in the CRC Handbook of Chemistry and Physics.
But before you look, here are some back-of-the-envelope estimates.
When heat is lost to the air, some is absorbed by nitrogen, some is absorbed by oxygen, and a tiny amount is absorbed by argon, carbon dioxide, water vapor, and trace gases. You can write
where xO2 and xN2 are moles of oxygen and moles of nitrogen per mole of air, and Cp(O2) and Cp(N2) are the constant pressure molar heat capacites for pure oxygen and nitrogen gases.Heat absorbed by one mole of air = heat absorbed by O2 + heat absorbed by N2 + ... = xO2Cp(O2) 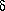 T
T
+ xN2Cp(N2) 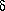 T
+ ...
T
+ ...
Assume that air is 21% oxygen, and 79% nitrogen by volume. If you can assume that the air behaves ideally, Avogadro's law says that the volume fraction for each gas is also its mole fraction. Since the heat absorbed by one mole of air should be Cp(air) times the change in temperature, you should be able to quickly estimate the heat capacity of air given Cp data for oxygen and nitrogen at the temperature you're interested in.
Assuming again that the air behaves ideally, the mole density (moles per unit volume) of air should be P/RT. You can convert the the mole density to a mass density using the molecular weight of air. The average molecular weight of a mixture is easy to calculate if you know the mole fractions of each component in the mixture:
M(mix) = x1M1 + x2M2 +...
where xi and Mi are the mole fractions and molecular weights for the i-th component in the mixture. This is exactly how average atomic weights are computed from isotopic masses and abundances...
General Chemistry Online! How can the heat capacity of air be estimated?
Copyright © 1997-2010 by Fred Senese
Comments & questions to fsenese@frostburg.edu
Last Revised 02/23/18.URL: http://antoine.frostburg.edu/chem/senese/101/thermo/faq/heat-capacity-air.shtml